Pythonゲームプログラミング #6 衝突判定
gist消してしまったので
代わりにこのリポジトリを参考にしてください
#0 環境構築
#1 メインループ
#2 画像表示
#3 アニメーション
#4 キー入力
#5 サウンド
#6 衝突判定
#7 ステートマシン
#8 マップチップ
#9 スクロール
衝突判定
pygameを使ったゲームプログラミングについて説明していきます。
- Windows10
- Python3.6.1
- pygame1.9.3
今回は衝突判定です。
バウンディングボリューム

ゲームプログラミングではフレーム処理をなるべく時間をかけずに終わらせる必要があるため、 ゲーム内のオブジェクトの衝突判定はバウンディングボリュームとよばれる幾何学形状に簡略化しておこなわれることがほとんどです。 今回は最も簡単な衝突判定の一つである円と円の判定を実装してみます。
サンプルコード
実行結果
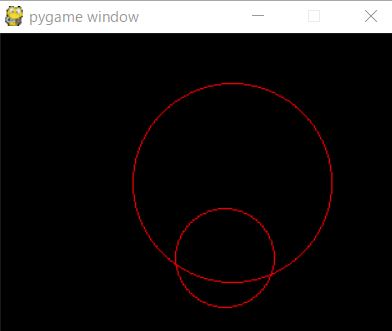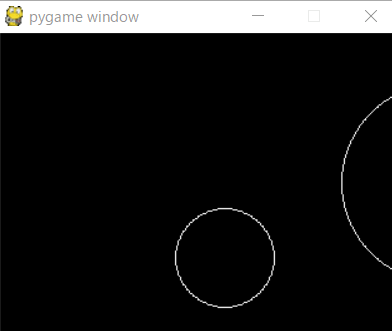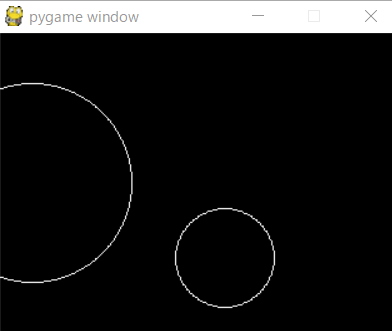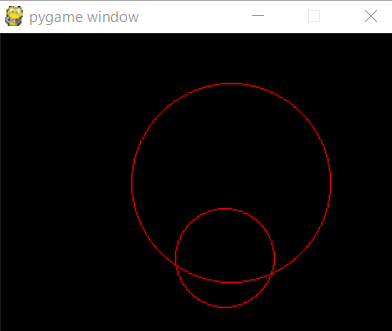
解説
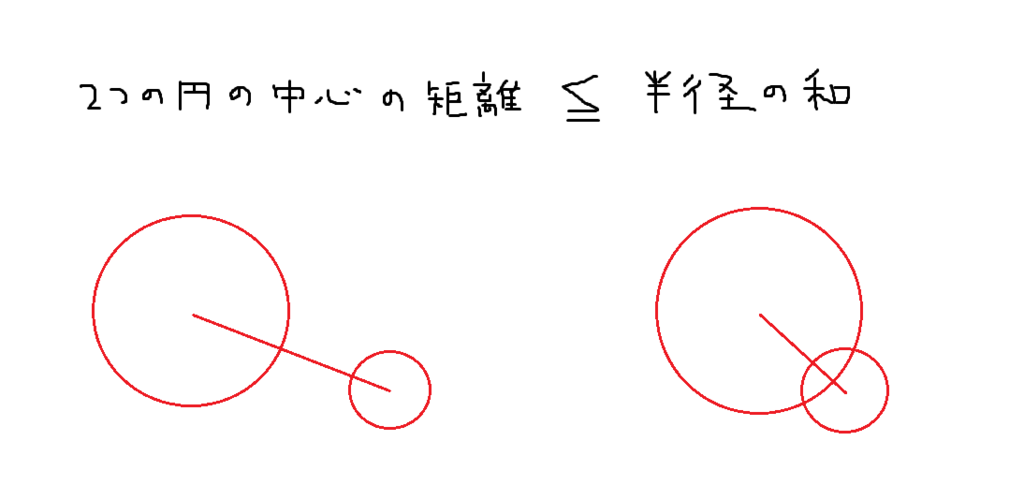
画像を見てもわかるとおり、円と円が衝突しているかは「2つの円の中心距離」が「2つの円の半径の和」以下かどうかで判定することができます。 2つの円の半径と位置はパラメータで管理しますが、距離は計算で求める必要があります。 2点の座標間の距離は高校生で習う「ベクトル」というものを使うと簡単に求められるのですが、pygameは2Dなのでピタゴラスの定理で説明します。
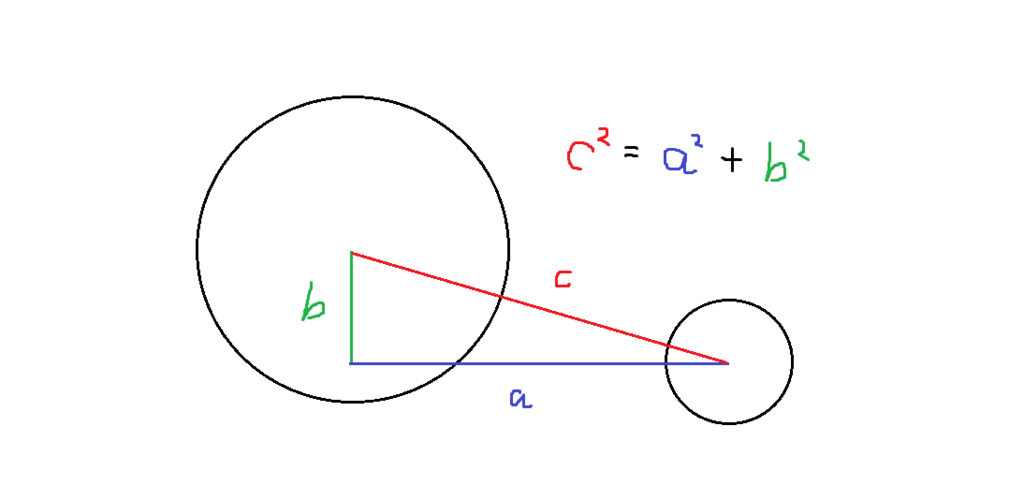
2Dの直交座標系上では、2点間の距離は直角三角形の斜辺の長さと同じものとして考えることができます。 ピタゴラスの定理より「斜辺の長さの2乗(c^2)」は「底辺の長さの2乗(a^2)と高さの2乗(b^2)の和」と等しい、つまり
c^2 = a^2 + b^2
という式が成り立ちます。平方根を求めるのは計算コストがかかるので、比較する半径の和も2乗して考えると、 円と円の衝突判定の式は下記のように「半径の和の2乗」と「斜辺の2乗」を比較したもので実現することができます。
r = r0 + r1 # 二つの半径の和 a = x0 - x1 # 底辺(2乗して判定するのでマイナスでも大丈夫) b = y0 - y1 # 高さ(2乗して判定するのでマイナスでも大丈夫) # 斜辺の長さが半径以下なら? if (a * a + b * b) <= (r * r): print('当たってる') else: print('当たってない')